Page 104 - Read Online

Mai et al. Intell Robot 2023;3(4):466-84 I http://dx.doi.org/10.20517/ir.2023.37 Page 11 of 19

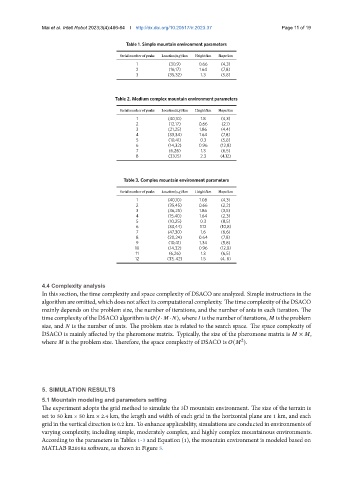
Table 1. Simple mountain environment parameters
Serial number of peaks Location(x,y)/km Height/km Slope/km
1 (30,9) 0.66 (4,3)
2 (16,17) 1.64 (7,8)
3 (35,32) 1.3 (5,8)

Table 2. Medium complex mountain environment parameters

Serial number of peaks Location(x,y)/km Height/km Slope/km
1 (40,10) 1.8 (4,3)
2 (12,17) 0.66 (2,1)
3 (21,25) 1.86 (4,4)
4 (33,34) 1.64 (7,8)
5 (10,41) 0.3 (5,8)
6 (14,32) 0.96 (12,8)
7 (6,26) 1.3 (6,5)
8 (33,15) 2.3 (4,12)

Table 3. Complex mountain environment parameters
Serial number of peaks Location(x,y)/km Height/km Slope/km
1 (40,10) 1.08 (4,3)
2 (35,45) 0.66 (2,2)
3 (36,25) 1.86 (3,5)
4 (15,40) 1.64 (2,3)
5 (10,25) 0.3 (8,5)
6 (33,44) 1.12 (10,8)
7 (47,30) 1.6 (6,6)
8 (20,24) 0.64 (7,8)
9 (10,41) 1.34 (5,8)
10 (14,32) 0.96 (12,8)
11 (6,26) 1.3 (6,5)
12 (33, 42) 1.5 (4, 8)

4.4 Complexity analysis
In this section, the time complexity and space complexity of DSACO are analyzed. Simple instructions in the
algorithmareomitted, whichdoesnotaffectitscomputationalcomplexity. ThetimecomplexityoftheDSACO
mainly depends on the problem size, the number of iterations, and the number of ants in each iteration. The
time complexity of the DSACO algorithm is ( · · ), where is the number of iterations, is the problem
size, and is the number of ants. The problem size is related to the search space. The space complexity of
DSACO is mainly affected by the pheromone matrix. Typically, the size of the pheromone matrix is × ,
where is the problem size. Therefore, the space complexity of DSACO is ( ).
2

5. SIMULATION RESULTS
5.1 Mountain modeling and parameters setting
The experiment adopts the grid method to simulate the 3D mountain environment. The size of the terrain is
set to 50 km × 50 km × 2.4 km, the length and width of each grid in the horizontal plane are 1 km, and each
grid in the vertical direction is 0.2 km. To enhance applicability, simulations are conducted in environments of
varying complexity, including simple, moderately complex, and highly complex mountainous environments.
According to the parameters in Tables 1-3 and Equation (1), the mountain environment is modeled based on
MATLAB R2018a software, as shown in Figure 5.