Page 105 - Read Online

Page 12 of 19 Mai et al. Intell Robot 2023;3(4):466-84 I http://dx.doi.org/10.20517/ir.2023.37

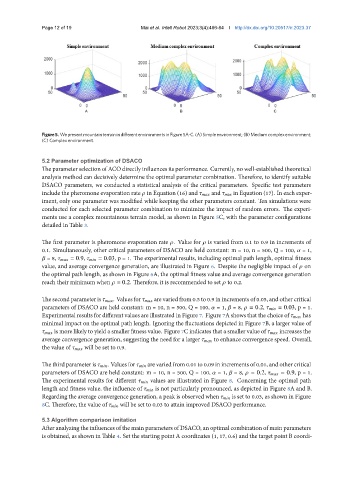
Figure5. We present mountain terrain in different environmentsin Figure 5A-C.(A) Simple environment; (B)Medium complexenvironment;
(C) Complex environment.

5.2 Parameter optimization of DSACO
The parameter selection of ACO directly influences its performance. Currently, no well-established theoretical
analysis method can decisively determine the optimal parameter combination. Therefore, to identify suitable
DSACO parameters, we conducted a statistical analysis of the critical parameters. Specific test parameters
include the pheromone evaporation rate in Equation (16) and and in Equation (17). In each exper-
iment, only one parameter was modified while keeping the other parameters constant. Ten simulations were
conducted for each selected parameter combination to minimize the impact of random errors. The experi-
ments use a complex mountainous terrain model, as shown in Figure 5C, with the parameter configurations
detailed in Table 3.

The first parameter is pheromone evaporation rate . Value for is varied from 0.1 to 0.9 in increments of
0.1. Simultaneously, other critical parameters of DSACO are held constant: m = 10, n = 500, Q = 100, = 1,
= 8, = 0.9, = 0.03, p = 1. The experimental results, including optimal path length, optimal fitness
value, and average convergence generation, are illustrated in Figure 6. Despite the negligible impact of on
the optimal path length, as shown in Figure 6A, the optimal fitness value and average convergence generation
reach their minimum when = 0.2. Therefore, it is recommended to set to 0.2.

The secondparameteris . Valuesfor are varied from 0.5 to 0.9 in incrementsof0.05, and other critical
parameters of DSACO are held constant: m = 10, n = 500, Q = 100, = 1, = 8, = 0.2, = 0.03, p = 1.
Experimental results for different values are illustrated in Figure 7. Figure 7A shows that the choice of has
minimal impact on the optimal path length. Ignoring the fluctuations depicted in Figure 7B, a larger value of
is more likely to yield a smaller fitness value. Figure 7C indicates that a smaller value of increases the
average convergence generation, suggesting the need for a larger to enhance convergence speed. Overall,
the value of will be set to 0.9.

The third parameter is . Values for are varied from 0.01 to 0.09 in increments of 0.01, and other critical
parameters of DSACO are held constant: m = 10, n = 500, Q = 100, = 1, = 8, = 0.2, = 0.9, p = 1.
The experimental results for different values are illustrated in Figure 8. Concerning the optimal path
length and fitness value, the influence of is not particularly pronounced, as depicted in Figure 8A and B.
Regarding the average convergence generation, a peak is observed when is set to 0.03, as shown in Figure
8C. Therefore, the value of will be set to 0.03 to attain improved DSACO performance.

5.3 Algorithm comparison imitation
After analyzing the influences of the main parameters of DSACO, an optimal combination of main parameters
is obtained, as shown in Table 4. Set the starting point A coordinates (1, 17, 0.6) and the target point B coordi-