Page 86 - Read Online

Liu et al. Intell Robot 2024;4(3):256-75 I http://dx.doi.org/10.20517/ir.2024.17 Page 270

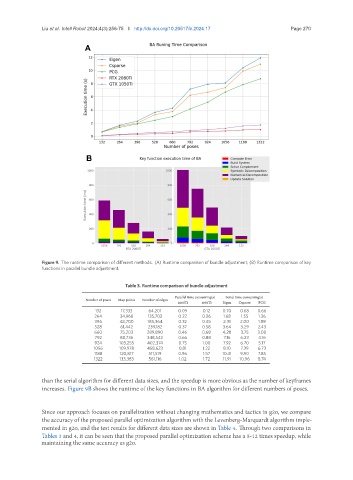
Figure 9. The runtime comparison of different methods. (A) Runtime comparison of bundle adjustment; (B) Runtime comparison of key
functions in parallel bundle adjustment.

Table 3. Runtime comparison of bundle adjustment
Parallel time consuming(s) Serial time consuming(s)
Number of poses Map points Number of edges
2080Ti 1050Ti Eigen Csparse PCG
132 17,333 64,201 0.09 0.12 0.70 0.68 0.66
264 34,968 135,702 0.22 0.26 1.68 1.55 1.36
396 48,700 185,364 0.32 0.45 2.31 2.00 1.88
528 61,442 239,182 0.37 0.58 3.64 3.29 2.43
660 75,203 289,890 0.46 0.68 4.28 3.75 3.00
792 88,736 348,542 0.66 0.88 7.16 6.23 4.16
924 103,255 402,374 0.75 1.00 7.92 6.70 5.17
1056 109,978 458,623 0.81 1.22 8.10 7.39 6.73
1188 120,817 511,519 0.96 1.57 10.41 9.90 7.85
1322 133,383 561,116 1.02 1.72 11.91 10.96 8.74

than the serial algorithm for different data sizes, and the speedup is more obvious as the number of keyframes
increases. Figure 9B shows the runtime of the key functions in BA algorithm for different numbers of poses.

Since our approach focuses on parallelization without changing mathematics and tactics in g2o, we compare
the accuracy of the proposed parallel optimization algorithm with the Levenberg-Marquardt algorithm imple-
mented in g2o, and the test results for different data sizes are shown in Table 4. Through two comparisons in
Tables 3 and 4, it can be seen that the proposed parallel optimization scheme has a 5-12 times speedup, while
maintaining the same accuracy as g2o.