Page 17 - Read Online

Page 342 Zhang et al. Intell. Robot. 2025, 5(2), 333-54 I http://dx.doi.org/10.20517/ir.2025.17

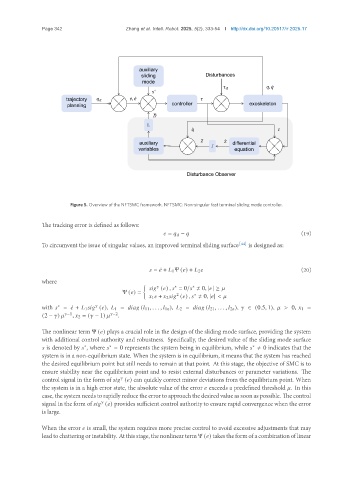
Figure 5. Overview of the NFTSMC framework. NFTSMC: Non-singular fast terminal sliding mode controller.

The tracking error is defined as follows:
= − (19)

To circumvent the issue of singular values, an improved terminal sliding surface [44] is designed as:

= ¤ + 1 Ψ ( ) + 2 (20)
where

( ) , = 0/ ≠ 0, | | ≥
∗
∗
Ψ ( ) = 2
1 + 2 ( ) , ≠ 0, | | <
∗

∗
with = ¤ + 1 ( ), 1 = ( 11 , . . . , 1 ), 2 = ( 21 , . . . , 2 ), ∈ (0.5, 1), > 0, 1 =
(2 − ) −1 , 2 = ( − 1) −2 .
The nonlinear term Ψ ( ) plays a crucial role in the design of the sliding mode surface, providing the system
with additional control authority and robustness. Specifically, the desired value of the sliding mode surface
is denoted by , where = 0 represents the system being in equilibrium, while ≠ 0 indicates that the
∗
∗
∗
system is in a non-equilibrium state. When the system is in equilibrium, it means that the system has reached
the desired equilibrium point but still needs to remain at that point. At this stage, the objective of SMC is to
ensure stability near the equilibrium point and to resist external disturbances or parameter variations. The
control signal in the form of ( ) can quickly correct minor deviations from the equilibrium point. When

the system is in a high error state, the absolute value of the error exceeds a predefined threshold . In this
case, thesystemneedstorapidlyreducetheerrortoapproachthedesiredvalueas soonaspossible. The control

signal in the form of ( ) provides sufficient control authority to ensure rapid convergence when the error
is large.
When the error is small, the system requires more precise control to avoid excessive adjustments that may
leadtochatteringorinstability. Atthisstage, thenonlinearterm Ψ ( ) takestheformofacombinationoflinear