Page 13 - Read Online

Page 338 Zhang et al. Intell. Robot. 2025, 5(2), 333-54 I http://dx.doi.org/10.20517/ir.2025.17

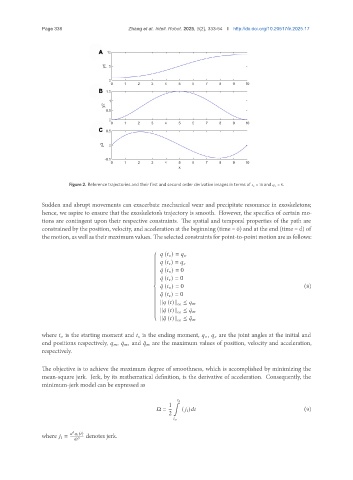
Figure 2. Reference trajectories and their first and second order derivative images in terms of = 10 and = 8.

Sudden and abrupt movements can exacerbate mechanical wear and precipitate resonance in exoskeletons;
hence, we aspire to ensure that the exoskeleton’s trajectory is smooth. However, the specifics of certain mo-
tions are contingent upon their respective constraints. The spatial and temporal properties of the path are
constrained by the position, velocity, and acceleration at the beginning (time = 0) and at the end (time = d) of
the motion, as well as their maximum values. The selected constraints for point-to-point motion are as follows:

 ( ) =




 ( ) =



 ¤ ( ) = 0



 ¤ ( ) = 0

 
¥ ( ) = 0 (8)


 ¥ ( ) = 0



 ≤
 k ( )k
 ∞


 k ¤ ( )k ≤ ¤
 ∞


 k ¥ ( )k ∞ ≤ ¥
where is the starting moment and is the ending moment, , are the joint angles at the initial and
end positions respectively, , ¤ , and ¥ are the maximum values of position, velocity and acceleration,

respectively.
The objective is to achieve the maximum degree of smoothness, which is accomplished by minimizing the
mean-square jerk. Jerk, by its mathematical definition, is the derivative of acceleration. Consequently, the
minimum-jerk model can be expressed as

¹
1
Ω = ( ) (9)
2

3
( )
where = denotes jerk.
3