Page 344 - Read Online

Kumar et al. Vessel Plus 2019;3:35 I http://dx.doi.org/10.20517/2574-1209.2019.006 Page 7 of 13

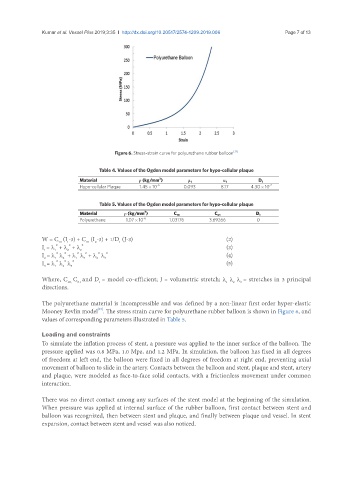
Figure 6. Stress-strain curve for polyurethane rubber balloon [13]

Table 4. Values of the Ogden model parameters for hypo-cellular plaque
3
Material ρ (kg/mm ) µ 1 α 1 D 1
Hypo-cellular Plaque 1.45 × 10 -6 0.093 8.17 4.30 × 10 -7

Table 5. Values of the Ogden model parameters for hypo-cellular plaque
3
Material ρ (kg/mm ) C 10 C 01 D 1
Polyurethane 1.07 × 10 -6 1.03176 3.69266 0

W = C (I -3) + C (I -3) + 1/D (J-3) (2)
01
2
1
1
10
2
2
2
I = λ + λ + λ (3)
2
1
2
1
2
2
2
2
2
2
I = λ λ + λ λ + λ λ (4)
2
3
1
2
3
1
2
2
2
I = λ λ λ 3 2 (5)
1
3
2
Where, C C and D = model co-efficient; J = volumetric stretch; λ λ λ = stretches in 3 principal
10,
01
1
3
2
1
directions.
The polyurethane material is incompressible and was defined by a non-linear first order hyper-elastic
[17]
Mooney Revlin model . The stress strain curve for polyurethane rubber balloon is shown in Figure 6, and
values of corresponding parameters illustrated in Table 5.
Loading and constraints
To simulate the inflation process of stent, a pressure was applied to the inner surface of the balloon. The
pressure applied was 0.8 MPa, 1.0 Mpa, and 1.2 MPa. In simulation, the balloon has fixed in all degrees
of freedom at left end, the balloon were fixed in all degrees of freedom at right end, preventing axial
movement of balloon to slide in the artery. Contacts between the balloon and stent, plaque and stent, artery
and plaque, were modeled as face-to-face solid contacts, with a frictionless movement under common
interaction.
There was no direct contact among any surfaces of the stent model at the beginning of the simulation.
When pressure was applied at internal surface of the rubber balloon, first contact between stent and
balloon was recognized, then between stent and plaque, and finally between plaque and vessel. In stent
expansion, contact between stent and vessel was also noticed.