Page 124 - Read Online

Peng et al. Intell Robot 2022;2(3):298­312 I http://dx.doi.org/10.20517/ir.2022.27 Page 308

3

2

1
0 2 4 6 8 10 12 14 16 18 20

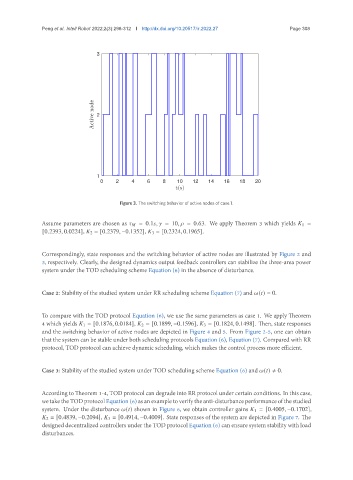
Figure 3. The switching behavior of active nodes of case 1.

Assume parameters are chosen as = 0.1 , = 10, = 0.63. We apply Theorem 3 which yields 1 =
[0.2393, 0.0224], 2 = [0.2379, −0.1352], 3 = [0.2324, 0.1965].

Correspondingly, state responses and the switching behavior of active nodes are illustrated by Figure 2 and
3, respectively. Clearly, the designed dynamics output feedback controllers can stabilize the three-area power
system under the TOD scheduling scheme Equation (6) in the absence of disturbance.

Case 2: Stability of the studied system under RR scheduling scheme Equation (7) and ( ) = 0.

To compare with the TOD protocol Equation (6), we use the same parameters as case 1. We apply Theorem
4 which yields 1 = [0.1876, 0.0184], 2 = [0.1899, −0.1596], 3 = [0.1824, 0.1498]. Then, state responses
and the switching behavior of active nodes are depicted in Figure 4 and 5. From Figure 2-5, one can obtain
that the system can be stable under both scheduling protocols Equation (6), Equation (7). Compared with RR
protocol, TOD protocol can achieve dynamic scheduling, which makes the control process more efficient.

Case 3: Stability of the studied system under TOD scheduling scheme Equation (6) and ( ) ≠ 0.

According to Theorem 1-4, TOD protocol can degrade into RR protocol under certain conditions. In this case,
wetaketheTODprotocolEquation(6)asanexampletoverifytheanti-disturbanceperformanceofthestudied
system. Under the disturbance ( ) shown in Figure 6, we obtain controller gains 1 = [0.4005, −0.1702],
2 = [0.4839, −0.2094], 3 = [0.4914, −0.4009]. State responses of the system are depicted in Figure 7. The
designed decentralized controllers under the TOD protocol Equation (6) can ensure system stability with load
disturbances.