Page 105 - Read Online

Li et al. Intell Robot 2022;2(1):89–104 I http://dx.doi.org/10.20517/ir.2022.02 Page 99

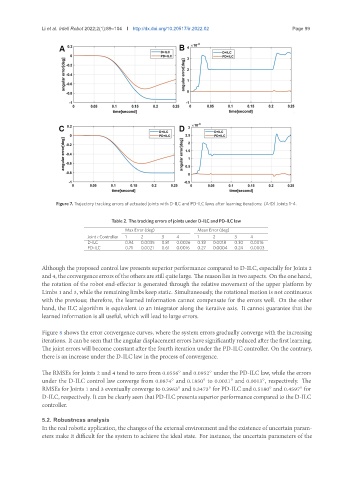
Figure 7. Trajectory tracking errors of actuated joints with D-ILC and PD-ILC laws after learning iterations: (A-D) Joints 1–4.

Table 2. The tracking errors of joints under D-ILC and PD-ILC law
Max Error (deg) Mean Error (deg)
Joint Controller 1 2 3 4 1 2 3 4
D-ILC 0.94 0.0035 0.81 0.0026 0.33 0.0018 0.30 0.0016
PD-ILC 0.71 0.0021 0.61 0.0016 0.27 0.0004 0.24 0.0003

Although the proposed control law presents superior performance compared to D-ILC, especially for Joints 2
and4, the convergenceerrors ofthe othersare still quite large. The reason lies in two aspects. On the onehand,
the rotation of the robot end-effector is generated through the relative movement of the upper platform by
Limbs 1 and 3, while the remaining limbs keep static. Simultaneously, the rotational motion is not continuous
with the previous; therefore, the learned information cannot compensate for the errors well. On the other
hand, the ILC algorithm is equivalent to an integrator along the iterative axis. It cannot guarantee that the
learned information is all useful, which will lead to large errors.

Figure 8 shows the error convergence curves, where the system errors gradually converge with the increasing
iterations. It can be seen that the angular displacement errors have significantly reduced after the first learning.
The joint errors will become constant after the fourth iteration under the PD-ILC controller. On the contrary,
there is an increase under the D-ILC law in the process of convergence.

The RMSEs for Joints 2 and 4 tend to zero from 0.0556 and 0.0952 under the PD-ILC law, while the errors
◦
◦
under the D-ILC control law converge from 0.0874 and 0.1850 to 0.0021 and 0.0013 , respectively. The
◦
◦
◦
◦
RMSEs for Joints 1 and 3 eventually converge to 0.3963 and 0.3473 for PD-ILC and 0.5180 and 0.4597 for
◦
◦
◦
◦
D-ILC, respectively. It can be clearly seen that PD-ILC presents superior performance compared to the D-ILC
controller.
5.2. Robustness analysis
In the real robotic application, the changes of the external environment and the existence of uncertain param-
eters make it difficult for the system to achieve the ideal state. For instance, the uncertain parameters of the