Page 106 - Read Online

Page 100 Li et al. Intell Robot 2022;2(1):89–104 I http://dx.doi.org/10.20517/ir.2022.02

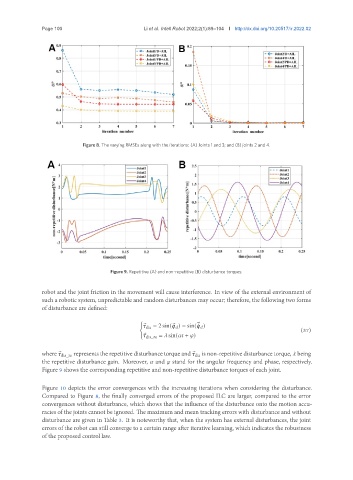
Figure 8. The varying RMSEs along with the iterations: (A) Joints 1 and 3; and (B) joints 2 and 4.

Figure 9. Repetitive (A) and non-repetitive (B) disturbance torques.

robot and the joint friction in the movement will cause interference. In view of the external environment of
such a robotic system, unpredictable and random disturbances may occur; therefore, the following two forms
of disturbance are defined:

{
® dis = 2 sin( ® ) − sin( ® ¤ )
(37)
® dis_re = sin( + )

where ® dis_re represents the repetitive disturbance torque and ® dis is non-repetitive disturbance torque, being
the repetitive disturbance gain. Moreover, and stand for the angular frequency and phase, respectively.
Figure 9 shows the corresponding repetitive and non-repetitive disturbance torques of each joint.

Figure 10 depicts the error convergences with the increasing iterations when considering the disturbance.
Compared to Figure 8, the finally converged errors of the proposed ILC are larger, compared to the error
convergences without disturbance, which shows that the influence of the disturbance onto the motion accu-
racies of the joints cannot be ignored. The maximum and mean tracking errors with disturbance and without
disturbance are given in Table 3. It is noteworthy that, when the system has external disturbances, the joint
errors of the robot can still converge to a certain range after iterative learning, which indicates the robustness
of the proposed control law.