Page 45 - Read Online

Page 110 Wu. Intell Robot 2021;1(2):99-115 I http://dx.doi.org/10.20517/ir.2021.11

−1
∂f /∂K [Hz/Nm⋅rad ]
1 act,2
−1
∂f /∂K [Hz/Nm⋅rad ] 7
1 act,1 0.96
0.94 6
600
600
0.92
500 5
0.9 400
400
0.88 z [mm] 4
z [mm] 200 0.86 200
300
0.84 3
100
0
0 0.82
2
−100 0.8
0.78 800 800
800 800 600 600 1
600 600 0.76 400 400
y [mm] 400 400 x [mm] y [mm] x [mm]
200 200 200 200
0 0 0 0
(a) (b)
Figure 6. Sensitivities of the first-order natural frequency to the joint stiffness: (a) Joint 1; and (b) Joint 2.

9
f [Hz] f [Hz]
2
1
8
8.5
600 600
500 7.5 500 8
400
400 300
z [mm] 300 7 z [mm] 200 7.5
200
100 6.5 100 7
0
0
−100 6 −100 6.5
800 800 800 800 6
600 600 5.5 600 600
400 400 400 400
y [mm] y [mm] 200 200 x [mm]
200 200 x [mm] 5.5
0 0 0 0
(a) (b)
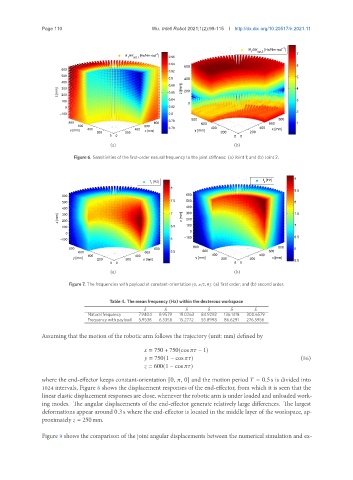
Figure 7. The frequencies with payload at constant-orientation [0, /2, 0]: (a) first order; and (b) second order.
Table 4. The mean frequency (Hz) within the dexterous workspace
¯ 1 ¯ 2 ¯ 3 ¯ 4 ¯ 5 ¯ 6
Natural frequency 7.9404 8.9579 19.0263 84.9292 136.1418 300.6579
Frequency with payload 5.9538 6.5358 15.2772 55.8998 86.6291 276.5956
Assuming that the motion of the robotic arm follows the trajectory (unit: mm) defined by

= 750 + 750(cos − 1)
= 750(1 − cos ) (56)
= 600(1 − cos )
where the end-effector keeps constant-orientation [0, , 0] and the motion period = 0.5 s is divided into
1024 intervals, Figure 8 shows the displacement responses of the end-effector, from which it is seen that the
linear elastic displacement responses are close, whenever the robotic arm is under loaded and unloaded work-
ing modes. The angular displacements of the end-effector generate relatively large differences. The largest
deformations appear around 0.3 s where the end-effector is located in the middle layer of the workspace, ap-
proximately = 250 mm.

Figure 9 shows the comparison of the joint angular displacements between the numerical simulation and ex-