Page 43 - Read Online

Page 108 Wu. Intell Robot 2021;1(2):99-115 I http://dx.doi.org/10.20517/ir.2021.11

f [Hz] f [Hz]
1 2
10.5 12
600 600 11.5
10
500 500 11
400 9.5 400 10.5
z [mm] 300 9 z [mm] 300 10
200
200
100 8.5 100 9.5
0 0 9
−100 8 −100 8.5
800 800 7.5 800 800 8
600 600 600 600
400 400 400 7.5
y [mm] 400 7 y [mm] x [mm]
200 200 x [mm] 200 200
0 0 0 0 7
(a) (b)
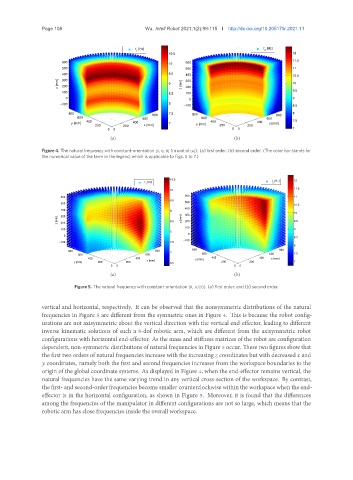
Figure 4. The natural frequency with constant-orientation [0, 0, 0] (in unit of rad): (a) first order; (b) second order. (The color bar stands for
the numerical value of the term in the legend, which is applicable to Figs. 5 to 7.)

10.5 12
f [Hz] f [Hz]
2
1
11.5
10
600
600 11
9.5 500
500
10.5
400
400 9
10
300
300
z [mm] 200 8.5 z [mm] 200 9.5
100
100 9
8
0
0
8.5
−100
−100 7.5
8
800 800 7 800 800
600 600 600 600 7.5
400 400 y [mm] 400 400 x [mm]
x [mm]
y [mm] 200 200 200 200 7
6.5
0 0 0 0
(a) (b)
Figure 5. The natural frequency with constant-orientation [0, /2 0]: (a) first order; and (b) second order.
vertical and horizontal, respectively. It can be observed that the nonsymmetric distributions of the natural
frequencies in Figure 5 are different from the symmetric ones in Figure 4. This is because the robot config-
urations are not axisymmetric about the vertical direction with the vertical end-effector, leading to different
inverse kinematic solutions of such a 5-dof robotic arm, which are different from the axisymmetric robot
configurations with horizontal end-effector. As the mass and stiffness matrices of the robot are configuration
dependent, non-symmetric distributions of natural frequencies in Figure 5 occur. These two figures show that
the first two orders of natural frequencies increase with the increasing coordinates but with decreased and
coordinates, namely both the first and second frequencies increases from the workspace boundaries to the
origin of the global coordinate systems. As displayed in Figure 4, when the end-effector remains vertical, the
natural frequencies have the same varying trend in any vertical cross-section of the workspace. By contrast,
the first- and second-order frequencies become smaller counterclockwise within the workspace when the end-
effector is in the horizontal configuration, as shown in Figure 5. Moreover, it is found that the differences
among the frequencies of the manipulator in different configurations are not so large, which means that the
robotic arm has close frequencies inside the overall workspace.