Page 96 - Read Online

Page 250 Shi et al. Art Int Surg 2024;4:247-57 https://dx.doi.org/10.20517/ais.2024.17

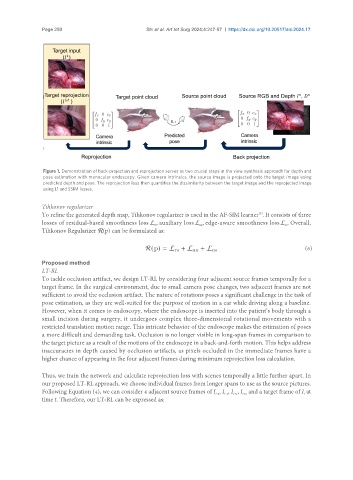
Figure 1. Demonstration of back-projection and reprojection serves as two crucial steps in the view synthesis approach for depth and
pose estimation with monocular endoscopy. Given camera intrinsics, the source image is projected onto the target image using
predicted depth and pose. The reprojection loss then quantifies the dissimilarity between the target image and the reprojected image
using L1 and SSIM losses.

Tihkonov regularizer
[9]
To refine the generated depth map, Tihkonov regularizer is used in the AF-SfM learner . It consists of three
losses of residual-based smoothness loss L , auxiliary loss L , edge-aware smoothness loss L . Overall,
ax
rs
es
Tihkonov Regularizer R(p) can be formulated as:
(6)

Proposed method
LT-RL
To tackle occlusion artifact, we design LT-RL by considering four adjacent source frames temporally for a
target frame. In the surgical environment, due to small camera pose changes, two adjacent frames are not
sufficient to avoid the occlusion artifact. The nature of rotations poses a significant challenge in the task of
pose estimation, as they are well-suited for the purpose of motion in a car while driving along a baseline.
However, when it comes to endoscopy, where the endoscope is inserted into the patient’s body through a
small incision during surgery, it undergoes complex three-dimensional rotational movements with a
restricted translation motion range. This intricate behavior of the endoscope makes the estimation of poses
a more difficult and demanding task. Occlusion is no longer visible in long-span frames in comparison to
the target picture as a result of the motions of the endoscope in a back-and-forth motion. This helps address
inaccuracies in depth caused by occlusion artifacts, as pixels occluded in the immediate frames have a
higher chance of appearing in the four adjacent frames during minimum reprojection loss calculation.

Thus, we train the network and calculate reprojection loss with scenes temporally a little further apart. In
our proposed LT-RL approach, we choose individual frames from longer spans to use as the source pictures.
Following Equation (4), we can consider 4 adjacent source frames of I , I , I , I and a target frame of I at
t
t+2
t-2
t-1
t+1
time t. Therefore, our LT-RL can be expressed as: