Page 48 - Read Online

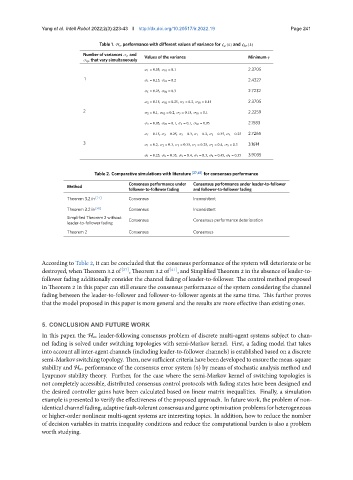
Yang et al. Intell Robot 2022;2(3):223­43 I http://dx.doi.org/10.20517/ir.2022.19 Page 241

Table 1. H ∞ performance with different values of variance for ( ) and 0 ( )
Number of variances and
0 that vary simultaneously Values of the variance Minimum ˆ
1 = 0.05, 01 = 0.1 2.3705
1 1 = 0.15, 01 = 0.2 2.4327

1 = 0.25, 02 = 0.3 2.7232
2 = 0.15, 02 = 0.25, 3 = 0.2, 03 = 0.15 2.3705
2 2 = 0.1, 02 = 0.2, 3 = 0.15, 03 = 0.1 2.2259

2 = 0.05, 02 = 0.1, 3 = 0.1, 03 = 0.05 2.1583
1 = 0.15, 2 = 0.25, 3 = 0.3, 1 = 0.2, 2 = 0.35, 3 = 0.25 2.7265
3 1 = 0.2, 2 = 0.3, 3 = 0.35, 1 = 0.25, 2 = 0.4, 3 = 0.3 3.1614
1 = 0.25, 2 = 0.35, 3 = 0.4, 1 = 0.3, 2 = 0.45, 3 = 0.35 3.9035

Table 2. Comparative simulations with literature [27,41] for consensus performance
Consensus performance under Consensus performance under leader-to-follower
Method
follower-to-follower fading and follower-to-follower fading
Theorem 3.2 in [27] Consensus Inconsistent

Theorem 3.2 in [41] Consensus Inconsistent
Simplified Theorem 2 without Consensus Consensus performance deterioration
leader-to-follower fading
Theorem 2 Consensus Consensus

According to Table 2, it can be concluded that the consensus performance of the system will deteriorate or be
destroyed, when Theorem 3.2 of [27] , Theorem 3.2 of [41] , and Simplified Theorem 2 in the absence of leader-to-
follower fading additionally consider the channel fading of leader-to-follower. The control method proposed
in Theorem 2 in this paper can still ensure the consensus performance of the system considering the channel
fading between the leader-to-follower and follower-to-follower agents at the same time. This further proves
that the model proposed in this paper is more general and the results are more effective than existing ones.

5. CONCLUSION AND FUTURE WORK
In this paper, the H ∞ leader-following consensus problem of discrete multi-agent systems subject to chan-
nel fading is solved under switching topologies with semi-Markov kernel. First, a fading model that takes
into account all inter-agent channels (including leader-to-follower channels) is established based on a discrete
semi-Markovswitchingtopology. Then, newsufficientcriteriahavebeendevelopedtoensurethemean-square
stability and H ∞ performance of the consensus error system (6) by means of stochastic analysis method and
Lyapunov stability theory. Further, for the case where the semi-Markov kernel of switching topologies is
not completely accessible, distributed consensus control protocols with fading states have been designed and
the desired controller gains have been calculated based on linear matrix inequalities. Finally, a simulation
example is presented to verify the effectiveness of the proposed approach. In future work, the problem of non-
identical channelfading, adaptivefault-tolerant consensus andgame optimizationproblems for heterogeneous
or higher-order nonlinear multi-agent systems are interesting topics. In addition, how to reduce the number
of decision variables in matrix inequality conditions and reduce the computational burden is also a problem
worth studying.