Page 28 - Read Online

Page 12 of 15 Sun et al. Complex Eng Syst 2022;2:17 I http://dx.doi.org/10.20517/ces.2022.48

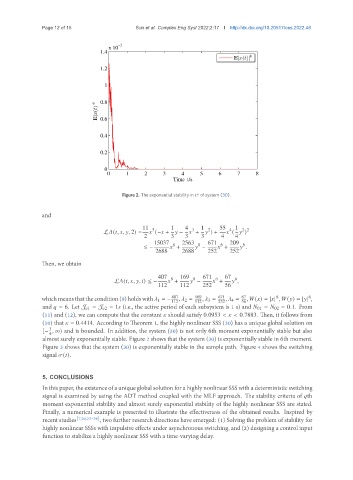
Figure 2. The exponential stability in of system (30).
6
and

11 5 1 4 3 1 2 55 4 1 2 2
L ( , , , 2) = (− + − + ) + ( )
2 3 3 3 4 4
15037 8 2563 8 671 6 209 6
≤ − + − + .
2688 2688 252 252
Then, we obtain

407 8 169 8 671 6 67 6
L ( , , , ) ≤ − + − + ,
112 112 252 56
407 169 671 67 8 8
whichmeansthatthecondition(9)holdswith 1 = − 112 , 2 = 112 , 3 = 252 , 4 = , ( ) = | | , ( ) = | | ,
56
and = 6. Let J 1 = J 2 = 1 (i.e., the active period of each subsystem is 1 s) and 01 = 02 = 0.1. From
(11) and (12), we can compute that the constant should satisfy 0.0953 < < 0.7883. Then, it follows from
(10) that = 0.4414. According to Theorem 1, the highly nonlinear SSS (30) has a unique global solution on
[− , ∞) and is bounded. In addition, the system (30) is not only 6th moment exponentially stable but also
3
4
almost surely exponentially stable. Figure 2 shows that the system (30) is exponentially stable in 6th moment.
Figure 3 shows that the system (30) is exponentially stable in the sample path. Figure 4 shows the switching
signal ( ).

5. CONCLUSIONS
Inthis paper, the existenceofa uniqueglobal solution for a highly nonlinear SSS with a deterministic switching
signal is examined by using the ADT method coupled with the MLF approach. The stability criteria of th
moment exponential stability and almost surely exponential stability of the highly nonlinear SSS are stated.
Finally, a numerical example is presented to illustrate the effectiveness of the obtained results. Inspired by
recent studies [7,20,33–36] , two further research directions have emerged: (1) Solving the problem of stability for
highly nonlinear SSSs with impulsive effects under asynchronous switching, and (2) designing a control input
function to stabilize a highly nonlinear SSS with a time-varying delay.