Page 12 - Read Online

Page 205 Zhu et al. Intell Robot 2022;2(3):200­222 I http://dx.doi.org/10.20517/ir.2022.13

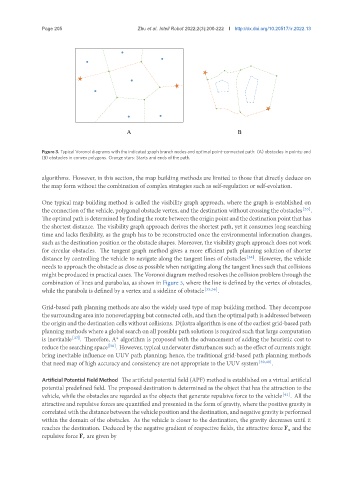
A B

Figure 3. Typical Voronoi diagrams with the indicated graph branch nodes and optimal point-connected path: (A) obstacles in points; and
(B) obstacles in convex polygons. Orange stars: Starts and ends of the path.

algorithms. However, in this section, the map building methods are limited to those that directly deduce on
the map form without the combination of complex strategies such as self-regulation or self-evolution.

One typical map building method is called the visibility graph approach, where the graph is established on
the connection of the vehicle, polygonal obstacle vertex, and the destination without crossing the obstacles [33] .
Theoptimalpathisdeterminedbyfindingtheroutebetweentheoriginpointandthedestinationpointthathas
the shortest distance. The visibility graph approach derives the shortest path, yet it consumes long searching
time and lacks flexibility, as the graph has to be reconstructed once the environmental information changes,
such as the destination position or the obstacle shapes. Moreover, the visibility graph approach does not work
for circular obstacles. The tangent graph method gives a more efficient path planning solution of shorter
distance by controlling the vehicle to navigate along the tangent lines of obstacles [34] . However, the vehicle
needs to approach the obstacle as close as possible when navigating along the tangent lines such that collisions
might be produced in practical cases. The Voronoi diagram method resolves the collision problem through the
combination of lines and parabolas, as shown in Figure 3, where the line is defined by the vertex of obstacles,
while the parabola is defined by a vertex and a sideline of obstacle [35,36] .

Grid-based path planning methods are also the widely used type of map building method. They decompose
the surrounding area into nonoverlapping but connected cells, and then the optimal path is addressed between
the origin and the destination cells without collisions. Dijkstra algorithm is one of the earliest grid-based path
planning methods where a global search on all possible path solutions is required such that large computation
is inevitable [37] . Therefore, A* algorithm is proposed with the advancement of adding the heuristic cost to
reduce the searching space [38] . However, typical underwater disturbances such as the effect of currents might
bring inevitable influence on UUV path planning; hence, the traditional grid-based path planning methods
that need map of high accuracy and consistency are not appropriate to the UUV system [39,40] .

Artificial Potential Field Method The artificial potential field (APF) method is established on a virtual artificial
potential predefined field. The proposed destination is determined as the object that has the attraction to the
vehicle, while the obstacles are regarded as the objects that generate repulsive force to the vehicle [41] . All the
attractive and repulsive forces are quantified and presented in the form of gravity, where the positive gravity is
correlatedwiththedistancebetweenthevehiclepositionandthedestination, andnegativegravityisperformed
within the domain of the obstacles. As the vehicle is closer to the destination, the gravity decreases until it
reaches the destination. Deduced by the negative gradient of respective fields, the attractive force F and the
repulsive force F are given by