Page 121 - Read Online

Guan et al. Intell Robot 2024;4(1):61-73 I http://dx.doi.org/10.20517/ir.2024.04 Page 69

Table 1. Benchmark functions
Function Common name Expression
Sphere ∑ 2
1 1 ( ) =
=1 ( )
Rosenbrock ∑ ( 2 2 ) 2
2 2 ( ) = =1 100 +1 − + ( − 1)
√
1 ∑ =1 2 1 ∑ cos(2 )
Ackley 3 ( ) = −20 −0.2 − + 20 +
3 =1
( ∑ ) 2
∑
4 Schwefel 4 ( ) = =1 =1
Rastrigin ∑ ( 2 )
5 5 ( ) = =1 − 10 cos (2 ) + 10

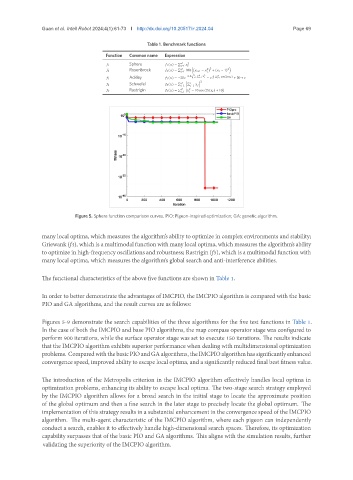
Figure 5. Sphere function comparison curves. PIO: Pigeon-inspired optimization; GA: genetic algorithm.

many local optima, which measures the algorithm’s ability to optimize in complex environments and stability;
Griewank (f4), which is a multimodal function with many local optima, which measures the algorithm’s ability
to optimize in high-frequency oscillations and robustness; Rastrigin (f5), which is a multimodal function with
many local optima, which measures the algorithm’s global search and anti-interference abilities.

The functional characteristics of the above five functions are shown in Table 1.

In order to better demonstrate the advantages of IMCPIO, the IMCPIO algorithm is compared with the basic
PIO and GA algorithms, and the result curves are as follows:

Figures 5-9 demonstrate the search capabilities of the three algorithms for the five test functions in Table 1.
In the case of both the IMCPIO and base PIO algorithms, the map compass operator stage was configured to
perform 900 iterations, while the surface operator stage was set to execute 150 iterations. The results indicate
that the IMCPIO algorithm exhibits superior performance when dealing with multidimensional optimization
problems. ComparedwiththebasicPIOandGAalgorithms,theIMCPIOalgorithmhassignificantlyenhanced
convergence speed, improved ability to escape local optima, and a significantly reduced final best fitness value.

The introduction of the Metropolis criterion in the IMCPIO algorithm effectively handles local optima in
optimization problems, enhancing its ability to escape local optima. The two-stage search strategy employed
by the IMCPIO algorithm allows for a broad search in the initial stage to locate the approximate position
of the global optimum and then a fine search in the later stage to precisely locate the global optimum. The
implementation of this strategy results in a substantial enhancement in the convergence speed of the IMCPIO
algorithm. The multi-agent characteristic of the IMCPIO algorithm, where each pigeon can independently
conduct a search, enables it to effectively handle high-dimensional search spaces. Therefore, its optimization
capability surpasses that of the basic PIO and GA algorithms. This aligns with the simulation results, further
validating the superiority of the IMCPIO algorithm.