Page 115 - Read Online

Guan et al. Intell Robot 2024;4(1):61-73 I http://dx.doi.org/10.20517/ir.2024.04 Page 63

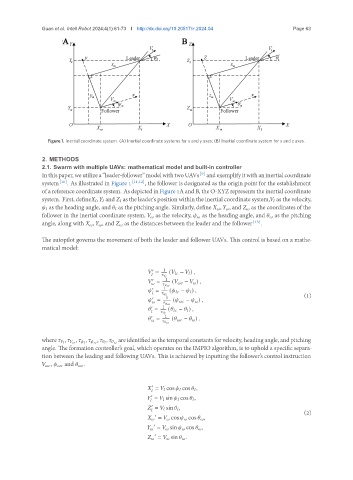
Figure 1. Inertial coordinate system. (A) Inertial coordinate systems for x and y axes; (B) Inertial coordinate system for x and z axes.

2. METHODS
2.1. Swarm with multiple UAVs: mathematical model and built-in controller
[9]
Inthispaper,weutilizea“leader-follower”modelwithtwoUAVs andexemplifyitwithaninertialcoordinate
system [10] . As illustrated in Figure 1 [11,12] , the follower is designated as the origin point for the establishment
of a reference coordinate system. As depicted in Figure 1A and B, the O-XYZ represents the inertial coordinate
system. First, define , and as the leader’s position within the inertial coordinate system, as the velocity,
as the heading angle, and as the pitching angle. Similarly, define , , and as the coordinates of the
follower in the inertial coordinate system, as the velocity, as the heading angle, and as the pitching
angle, along with , , and as the distances between the leader and the follower [13] .

The autopilot governs the movement of both the leader and follower UAVs. This control is based on a mathe-
matical model:

= 1 ( − ) ,
′

1
′
= ( − ) ,

= 1 ( − ) ,
′
(1)
1
= ( − ) ,
′

′
= 1 ( − ) ,

1
= ( − ) .
′

areidentifiedasthetemporalconstantsforvelocity, headingangle, andpitching
where , , , , ,
angle. The formation controller’s goal, which operates on the IMPIO algorithm, is to uphold a specific separa-
tion between the leading and following UAVs. This is achieved by inputting the follower’s control instruction
, and .
= cos cos ,
′

′
= sin cos ,

= sin ,
′
(2)
′
= cos cos ,
= sin cos ,
′
= sin .
′