Page 56 - Read Online

Harib et al. Intell Robot 2022;2(1):37-71 https://dx.doi.org/10.20517/ir.2021.19 Page 51

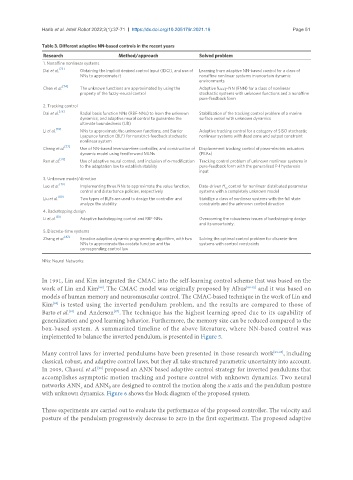
Table 3. Different adaptive NN-based controls in the recent years
Research Method/approach Solved problem
1. Nonaffine nonlinear systems
[73]
Dai et al. Obtaining the implicit desired control input (IDCI), and use of Learning from adaptive NN-based control for a class of
NNs to approximate it nonaffine nonlinear systems in uncertain dynamic
environments
[74]
Chen et al. The unknown functions are approximated by using the Adaptive fuzzy-NN (FNN) for a class of nonlinear
property of the fuzzy-neural control stochastic systems with unknown functions and a nonaffine
pure-feedback form
2. Tracking control
[75]
Dai et al. Radial basis function NNs (RBF-NNs) to learn the unknown Stabilization of the tracking control problem of a marine
dynamics, and adaptive neural control to guarantee the surface vessel with unknown dynamics
ultimate boundedness (UB)
Li et al. [76] NNs to approximate the unknown functions, and Barrier Adaptive tracking control for a category of SISO stochastic
Lyapunov function (BLF) for nonstrict-feedback stochastic nonlinear systems with dead zone and output constraint
nonlinear system
[77]
Cheng et al. Use of NN-based inversion-free controller, and construction of Displacement tracking control of piezo-electric actuators
dynamic model using feedforward MLNs (PEAs)
Ren et al. [78] Use of adaptive neural control, and inclusion of σ-modification Tracking control problem of unknown nonlinear systems in
to the adaptation law to establish stability pure-feedback form with the generalized P-I hysteresis
input
3. Unknown model/direction
Luo et al. [79] Implementing three NNs to approximate the value function, Date-driven H control for nonlinear distributed parameter
∞
control and disturbance policies, respectively systems with a completely unknown model
Liu et al. [80] Two types of BLFs are used to design the controller and Stabilize a class of nonlinear systems with the full state
analyze the stability constraints and the unknown control direction
4. Backstepping design
[81]
Li et al. Adaptive backstepping control and RBF-NNs. Overcoming the robustness issues of backstepping design
and its uncertainty.
5. Discrete-time systems
[82]
Zhang et al. Iterative adaptive dynamic programming algorithm, with two Solving the optimal control problem for discrete-time
NNs to approximate the costate function and the systems with control constraints
corresponding control law
NNs: Neural Networks.

In 1991, Lin and Kim integrated the CMAC into the self-learning control scheme that was based on the
work of Lin and Kim . The CMAC model was originally proposed by Albus [89-92] and it was based on
[88]
models of human memory and neuromuscular control. The CMAC-based technique in the work of Lin and
[88]
Kim is tested using the inverted pendulum problem, and the results are compared to those of
Barto et al. and Anderson . The technique has the highest learning speed due to its capability of
[83]
[87]
generalization and good learning behavior. Furthermore, the memory size can be reduced compared to the
box-based system. A summarized timeline of the above literature, where NN-based control was
implemented to balance the inverted pendulum, is presented in Figure 5.

Many control laws for inverted pendulums have been presented in those research work [93-95] , including
classical, robust, and adaptive control laws, but they all take structured parametric uncertainty into account.
In 2009, Chaoui et al. proposed an ANN based adaptive control strategy for inverted pendulums that
[96]
accomplishes asymptotic motion tracking and posture control with unknown dynamics. Two neural
networks ANN and ANN are designed to control the motion along the x axis and the pendulum posture
x
θ
with unknown dynamics. Figure 6 shows the block diagram of the proposed system.

Three experiments are carried out to evaluate the performance of the proposed controller. The velocity and
posture of the pendulum progressively decrease to zero in the first experiment. The proposed adaptive