Page 27 - Read Online

Li et al. Intell Robot 2023;3(2):213-21 I http://dx.doi.org/10.20517/ir.2023.13 Page 219

1
1

0
0

G 1 G 2
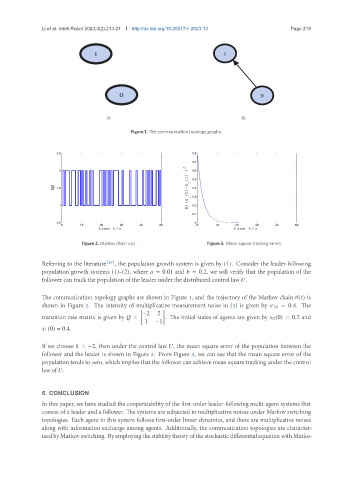
Figure 1. The communication topology graphs.

2.5 0.8
0.7
2 0.6

θ(t) 1.5 E||x 1 (t)−x 0 (t)|| 2 0.5
0.4
0.3
1 0.2
0.1
0.5 0
0 10 20 30 40 50 0 10 20 30 40 50
time t/s time t/s
Figure 2. Markov chain ( ). Figure 3. Mean square tracking errors.

Referring to the literature [29] , the population growth system is given by (1). Consider the leader-following
population growth systems (1)-(2), where = 0.01 and = 0.2, we will verify that the population of the
follower can track the population of the leader under the distributed control law .

The communication topology graphs are shown in Figure 1, and the trajectory of the Markov chain ( ) is
shown in Figure 2. The intensity of multiplicative measurement noise in (3) is given by 10 = 0.4. The

−2 2
transition rate matrix is given by = . The initial states of agents are given by 0 (0) = 0.2 and
1 −1
1 (0) = 0.4.

If we choose = −2, then under the control law , the mean square error of the population between the
follower and the leader is shown in Figure 3. From Figure 3, we can see that the mean square error of the
population tends to zero, which implies that the follower can achieve mean square tracking under the control
law of .

6. CONCLUSION
In this paper, we have studied the cooperatability of the first-order leader-following multi-agent systems that
consist of a leader and a follower. The systems are subjected to multiplicative noises under Markov switching
topologies. Each agent in this system follows first-order linear dynamics, and there are multiplicative noises
along with information exchange among agents. Additionally, the communication topologies are character-
ized by Markov switching. By employing the stability theory of the stochastic differential equation with Marko-