Page 50 - Read Online

Harib et al. Intell Robot 2022;2(1):37-71 https://dx.doi.org/10.20517/ir.2021.19 Page 45

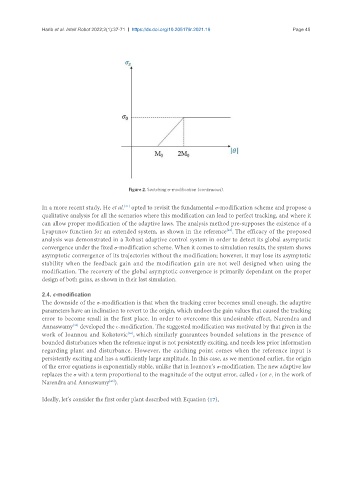
Figure 2. Switching σ-modification (continuous).

[41]
In a more recent study, He et al. opted to revisit the fundamental σ-modification scheme and propose a
qualitative analysis for all the scenarios where this modification can lead to perfect tracking, and where it
can allow proper modification of the adaptive laws. The analysis method pre-supposes the existence of a
Lyapunov function for an extended system, as shown in the reference . The efficacy of the proposed
[42]
analysis was demonstrated in a Robust adaptive control system in order to detect its global asymptotic
convergence under the fixed σ-modification scheme. When it comes to simulation results, the system shows
asymptotic convergence of its trajectories without the modification; however, it may lose its asymptotic
stability when the feedback gain and the modification gain are not well designed when using the
modification. The recovery of the global asymptotic convergence is primarily dependant on the proper
design of both gains, as shown in their last simulation.

2.4. ϵ-modification
The downside of the σ-modification is that when the tracking error becomes small enough, the adaptive
parameters have an inclination to revert to the origin, which undoes the gain values that caused the tracking
error to become small in the first place. In order to overcome this undesirable effect, Narendra and
[43]
Annaswamy developed the ϵ-modification. The suggested modification was motivated by that given in the
work of Ioannou and Kokotovic , which similarly guarantees bounded solutions in the presence of
[36]
bounded disturbances when the reference input is not persistently exciting, and needs less prior information
regarding plant and disturbance. However, the catching point comes when the reference input is
persistently exciting and has a sufficiently large amplitude. In this case, as we mentioned earlier, the origin
of the error equations is exponentially stable, unlike that in Ioannou’s σ-modification. The new adaptive law
replaces the σ with a term proportional to the magnitude of the output error, called ϵ (or e in the work of
1
[43]
Narendra and Annaswamy ).
Ideally, let’s consider the first order plant described with Equation (17),